Unit 5: Teaching Energy & Momentum
Inquiry-Oriented Student Performance Objectives:
5.1 Work and Power
- Students will analyze various combinations of pulleys to determine the
relationship between the number of support strings and the mechanical advantage.
- Students will determine whether or not mechanical advantage of a pulley
represents “free” energy – getting something for nothing
– or is consistent with the conservation of energy principle that says
“work input equals work output” (less considerations due to friction).
- Students will analyze the efficiency of a pulley by comparing work input
with work output.
- Students will determine if the efficiency of a particular pulley combination
varies with load and, if so, determine that relationship empirically.
- Students will, given the definitions of power, work, efficiency, and mechanical
advantage, determine the power required to lift a given weight a certain height
in a certain period of time using a particular configuration of pulley with
an assumed efficiency.
5.2 Potential and Kinetic Energy
- Students will, given the definitions of potential energy due to gravity
(PEg), potential energy due to a spring (PEs), and kinetic energy (KE), determine
if and to what degree energy is conserved as it is translated from:
5.2.1.1 PEg to PEs
5.2.1.2 PEg to KE
5.2.1.3 PEs to PEg
5.2.1.4 PEs to KE
5.2.1.5 KE to PEg
5.2.1.6 KE to PEs
- Students will, using an air or dynamics track or other suitable instrument,
determine if and to what degree kinetic energy is conserved in a collision
between dynamics carts in the following situations:
5.2.2.1 Moving cart colliding with a stationary cart.
5.2.2.2 Moving cart colliding with a cart moving in the same direction.
5.2.2.3 Moving cart colliding with a cart moving in the opposite direction.
- Students will, using a rotational apparatus and suitable sensors, determine
the relationship between the moment of inertia and the symmetrically distributed
mass of a rotating object or more objects.
- Students will, using a rotational apparatus and suitable sensors, determine
the relationship between the moment of inertia and the symmetrical distribution
of the mass of the rotating object or objects.
- Students will combine the results of objectives 5.2.3 and 5.2.4 to determine
the general form of the moment of inertia for two “point” masses
– essentially a dumbbell.
- Students will drop same-size balls with different masses from varying heights
onto clay to determine the relationship between kinetic energy (the ability
to do work on the clay) and both mass and velocity of the falling ball.
5.3 Momentum
- Students will, using an air track with sleds or track with dynamics carts,
determine whether or not momentum is conserved in a variety of situations
involving linear collisions:
5.3.1.1 Moving cart colliding with a stationary cart.
5.3.1.2 Moving cart colliding with a cart moving in the same direction.
5.3.1.3 Moving cart colliding with a cart moving in the opposite direction.
- Students will, using an inclined plane (e.g., two abutting whiteboards, one slightly inclined), determine whether or not momentum is conserved in glancing
collisions involving two balls that result in non-linear reactions.
- Students will, using a force sensor, a dynamics cart, and a collision, determine the relationship between impulse and momentum.
- Students will, using the impulse momentum theory as a basis, design and
build a device that allows a raw egg to survive a fall from the height of
two stories onto concrete without breaking.
- Students will determine the relationship between torque, moment of inertia,
and angular acceleration for a given rotational object.
5.4 Machines
- Students will, given the definition of torque, study three classes of levers
to determine the rule of mechanical advantage, and will define and analyze
mechanical advantage in relation to a hypothesized ideal.
- Students will, given the definition of torque, study different wheel and
axle combinations to determine the rule of mechanical advantage, and will
define and analyze actual efficiency in relation to a hypothesized ideal.
- Students will study inclined planes to determine the rule of mechanical
advantage, and will define and analyze actual efficiency in relation to a
hypothesized ideal.
- Students will study the geometry of a C-clamp to calculate the mechanical
advantage, and will define and analyze actual efficiency in relation to a
hypothesized ideal.
- Students will study the wedge to determine rule of mechanical advantage,
and will define and analyze actual efficiency in relation to a hypothesized
ideal.
- Students will study gears, chains, and belts to determine rule of mechanical
advantage.
Resource Information for Teaching Simple Machines:
Background on Simple Machines:
A machine is a device that does work. Most machines consist of
a number of elements, such as gears and ball bearings, that work together in
a complex way. Nonetheless, no matter how complex they are, all machines are
based in some way on six types of simple machines. These six types of machines
are the lever, the wheel and axle, the pulley, the inclined plane, the wedge,
and the screw.
Lever. There are three basic types of levers, depending on
the relative positions of where the effort is applied, the position of the load,
and the position of the fulcrum. Levers are in a state of equilibrium when the
sum of the torques about the fulcrum is zero.
Wheel and axle. The wheel and axle is essentially a modified
lever, but it can move a load farther than a lever can. The center of the axle
serves as a fulcrum.
Pulley. A pulley is a wheel over which a rope or belt is passed.
It is also a form of the wheel and axle. Pulleys are often interconnected in
order to obtain considerable mechanical advantage.
Inclined plane. The inclined plane is a simple device that
hardly looks like a machine at all. The mechanical advantage increases as the
slope of the incline decreases. But the load will then have to be moved a greater
distance.
Wedge. The wedge is an adaptation of the inclined plane. It
can be used to raise a heavy load over a short distance or to split a log.
Screw. The screw is actually an inclined plane wrapped in a
spiral around a shaft. A jackscrew combines the usefulness of the screw and
the lever. The lever is used to turn the screw.
Principles of Machines:
Machines simply transmit mechanical work from one part of a device to another
part. A machine produces force and controls the direction and the motion of
force, but it cannot create energy. A machine's ability to do work is measured
by two factors. These are the (1) efficiency and the (2) mechanical advantage. While
machines can provide a mechanical advantage of greater than 1.0, no machine
can never do more work than the energy put into it. They always have efficiencies
of less than 1.0 due to internal friction.
Mechanical advantage. In machines that transmit only mechanical
energy, the ratio of the force exerted by the machine to the force applied to
the machine is known as mechanical advantage. Under mechanical advantage the
distance the load will be moved will be only be a fraction of the distance through
which the effort is applied.
Efficiency. The efficiency of a machine is the
ratio between the energy it supplies and the energy put into it. Although friction
can be decreased by oiling any sliding or rotating parts, all machines produce
some friction. A lever has a high efficiency. The work it puts out is almost
equal to the energy it receives, because the energy used up by friction is quite
small. On the other hand, an a pulley might be relatively inefficient due to
a considerably greater amount of internal friction.
Energy conservation. Ignoring for a moment the losses of energy due
to friction, the work done on a simple machine is the same as the work done
by the machine to perform some sort of task. Energy is equals energy out is
the efficiency is 100%.
Teaching about Simple Machines:
- Pulley
- Various configurations (1-4 support strings; graph number of support
strings versus force required to life a 1-kg mass; use 10-newton spring
scale)
- Investigate “something for nothing”; what is the relationship
between force and distance pulled?
- What is idealized relationship between work in and work out
- Identify fact that and its relationship with conservation of energy
principle.
- Define efficiency. (
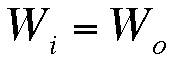 )
)
- Define mechanical advantage. (
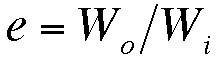 )
)
- Identify mechanical advantage of various configurations of ideal pulleys.
- Wheel and Axle
- For various configurations, measure force and distance.
- Relate configurations in pulleys to radii in wheel and axle configurations.
- Identify torque. (
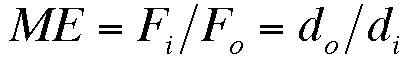 )
)
- Identify relationship of radii with mechanical advantage. (
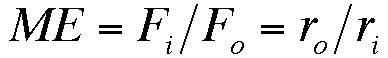 )
)
- The mechanical advantage of the windlass depends upon the ratio between
the radius of the axle and the distance from the center of the axle to
the crank handle.
- Levers
- Identify relationship between force and distance on both sides of fulcrum
for first-class lever.
- Relate to torques. (
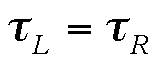 where
where 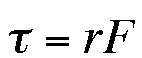 )
)
- Relate to mechanical advantage.
- Identify three classes of levers:
- First-class levers have the fulcrum located between the load and
the effort (LFE). If the two arms of the lever are
of equal length, the effort must be equal to the load. To lift 10
pounds, an effort of 10 pounds must be used. If the effort arm is
longer than the load arm, as with a crowbar, the hand applying the
effort travels farther and the effort is less than the load. SOCIAL
CONTEXT: Seesaws, crowbars, and equal-arm balances are examples of
a first class lever; a pair of scissors is a double lever of the first
class.
- Second-class levers have the load located between the fulcrum and
the effort (FLE). As in a wheel barrow, the axle
of the wheel is the fulcrum, the handles represent the position where
the effort is applied, and the load is placed between the hands and
the axle. The hands applying the effort travel a greater distance
and is less than the load. SOCIAL CONTEXT: In addition to a wheelbarrow,
a pry bar represents a second-class lever. A nutcracker is a double
lever of this class.
- Third-class levers have the effort located between the load and
the fulcrum (FEL). The hand applying the effort always
travels a shorter distance and must be greater than the load. SOCIAL
CONTEXT: The forearm is a third-class lever. The hand holding the
weight is lifted by the bicep muscles of the upper arm that is attached
to the forearm near the elbow. The elbow joint is the fulcrum.
- Compound levers combine two or more levers, usually
to decrease the effort. By applying the principle of the compound lever,
a person could use the weight of one hand to balance a load weighing a
ton.
- Law of Equilibrium
A lever is in equilibrium when the effort and the load balance each other;
that is, the sum of the torques equals zero. The effort multiplied by
the length of the effort arm equals the load multiplied by the length
of the load arm.
- Inclined Plane. The mechanical advantage of an inclined
plane is the length of the incline divided by the vertical rise, the so-called
run-to-rise ratio. The mechanical advantage increases as the slope of the
incline decreases, but then the load will have to be moved a greater distance.
Again, work in equals work out in an entirely efficient system. Friction will
be large if objects are slide along the surface of the inclined plane. Efficiency
can be increase by using rollers in conjunction with the inclined plane.
- Screw. The mechanical advantage of a screw is ideally
the ratio of the circumference of the screw to the distance it advances during
each revolution. Machine screws, working their way through a nut, can be relatively
efficient. Wood screws tend to be anything but 100% efficient as considerable
amounts of energy are lost to friction and the displacement of matter. A jackscrew,
such as those used to raise homes and other structures, combines the usefulness
of the screw and the lever. The lever is used to turn the screw. The mechanical
advantage of a jackscrew is quite high.
- Wedge. The mechanical advantage of a wedge depends on
the angle of the thin end. The smaller the angle, the less the force required
to move the wedge a given distance through, say, a log. At the same time,
the amount of splitting is decreased with smaller angles.
Online Resources:
Hippocampus.org - see the numerous physics videos for every conceivable physics topic
Annenburg/CPB Video on Demand - see especially the 52-part series Mechanical Universe.
Return to PHY 312 course syllabus.
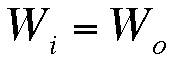 )
)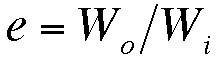 )
)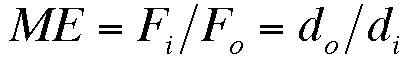 )
)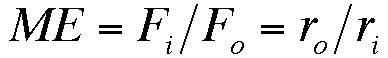 )
)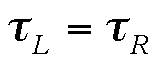 where
where 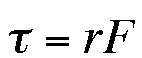 )
)